In the Vision article we talked about our goal to create a “Thinking Machine”, that is, an artificial intelligence capable of passing the Turing test. If you have not yet read the Vision section, we propose that you do so now.
Initially we started by designing a new class of programming language that we thought was more appropriate to implement Linear Genetic Programming. This new language has the property that each instruction can be transformed, up to a certain extent, continuously into a different instruction. A scalar factor alpha controls the transformation. We coined this new programming language CPL (Continuous Programming Language). As an example, consider the instruction x=1. With alpha = 0, x is left unchanged (equivalent to the NOP instruction). For alpha=0.5, x is the mean between the current value of x and 1. Finally for alpha=1, x is equal to 1.

Linear Genetic Programming
We then refined our genetic engine (mutations, crossover, migrations). To make sure that we have already reached state of the art performance, we benchmarked our engine against a standard classification problem (see Brameier and Banzhaf “A Comparison of Linear Genetic Programming and Neural Networks in Medical Data Mining”, 2001) and ran our genetic engine on the medical data set. The performance testing against the benchmark improved the genetic engine in many ways. We were able to use metagenetic methods to tune the many genetic parameters (mutation rate, population sizes, etc) . We were also able to visualize the populations to get a sense of what was going on as they evolved.
The picture below is a graphic representation of an entire population: each column represents a program, each color represents a different class of instruction (arithmetic, memory, flow control, etc) and the individuals are sorted based on their fitness, with the best one on the full left. We can see for instance that in this population the best individuals are similar (horizontal lines of a single color on the left indicate that the individuals, i.e. vertical lines, are similar) and that individuals with low fitness are tend to fewer number of instructions as indicated by the black spikes on the right side of the plot.

At this stage one of the open questions was: how likely is it that LGP (Linear Genetic Programming) will evolve code implementing the concept of neurons and getting us to an artificial intelligence? From our experience, we realized that this was extremely unlikely. We therefore decided to help the system by embedding the concept of neurons into the basic system. For this purpose, we introduced the concept of ”metaneuron”, a structural element whose behavior (meaning its relaxation and learning properties) would be defined by an LGP evolved program. The concepts of metaneurons is commonly used in neural networks for artificial intelligence. However, in our case the concept is much more elaborate as it is combined with LGP.
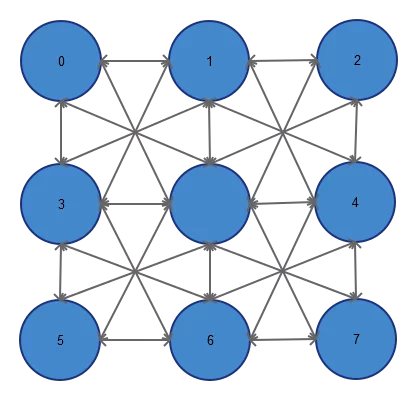
As a first check, we tested the genericity of the approach by training a multilayer network on the XOR problem. Although we were able to find solutions for the XOR problems, we also observed that the metaneurons were not collaborating as in a neural network to solve problems. Several improvements were necessary, such as imposing a grid topology (see figure below) with 8 neighbor connections (this assures that information has to travel into and through the network to reach the output).
Next, we checked for cases of chaotic behavior, situations where changing boundary conditions, for instance one single connection weight, would dramatically increase the system error. Given that healthy biological neural networks are very robust to changes that naturally occur in all physical systems we want our system to have the same characteristic. The next requirement was defined as the capacity of “true” learning. This, although obvious, is extremely important as in many instances we found that the LGP programs just secretly stored several internal states useful when executing the program. Instead of learning, the programs just tested the various sets of pre-stored states until the error was good.
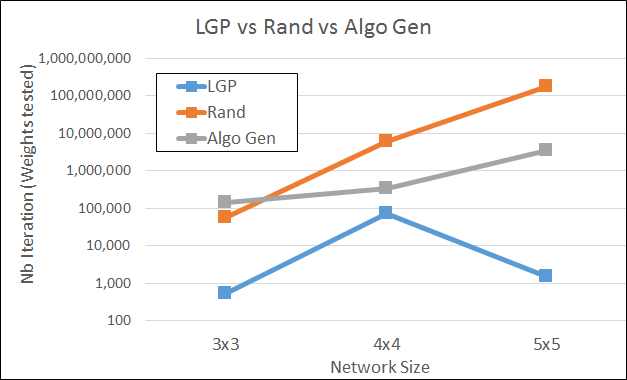
To avoid this pitfall effectively we used a training set and a distinct test set. Consequently we designed the training set with 8 Boolean 2-inputs functions f1(i,j), f2(i,j)… f8(i,j). For instance, f1 could be the XOR problem. The genetic engine has then to find a code such that the metaneurons can learn any of those functions. Once the learning program is found, its learning performance is then assessed using a test set made of 8 other Boolean functions f9,..f16. The number of training sets and training set size has of course a direct impact on computational complexity and required us to increase the computation speed by several orders of magnitude. Basic computational speedup was reached by hardcoding the relaxation function in C++ (using integrate and fire) and only evolved the learning program with LGP. Using several hours of computing on over 100 cores, the system found learning algorithms for different network sizes (3×3, 4×4, and 5×5). The found learning programs vastly outperformed state of the art optimization techniques. They were 2,300 times faster than the genetic algorithmic search and 100,000 times faster than a random search.
Disruption for complex problems
Is our approach to reach artificial intelligence disruptive? Yes, it is. Are our results disruptive? Yes, they are. We are therefore motivated to take this to the next level. Future works will focus on extending this approach to more complex problems by using more neurons, more complex topology and constructing more powerful instructions for our LGP language. At this stage we are still far from having a thinking machine in our hands, however, we feel that the our tools become more and more powerful and that we are on the right track to tackle the problem of artificial intelligence.
Subscribe to stay tuned as we continue our quest for knowledge and push the boundaries of science.
